人需要了解自己的局限性——Dirty Harry
你的资源受限了。你只有那么点的时间和钱去工作,还需要保持你的知识、技能和工具更新迭代。你也只能是更努力、快速、灵活、更长时间地工作。你的工具也如此而已。你的目标平台性能也就如此。因此你不得不敬畏这种资源限制。
如何敬畏呢?了解你自己,了解你周围的人,了解你的预算,了解你所拥有的。尤其是作为一个软件工程师,应该了解你的数据结构和算法的时间/空间复杂度,你系统的架构及典型性能。你的工作就是创造一次软件和系统的最佳结合。
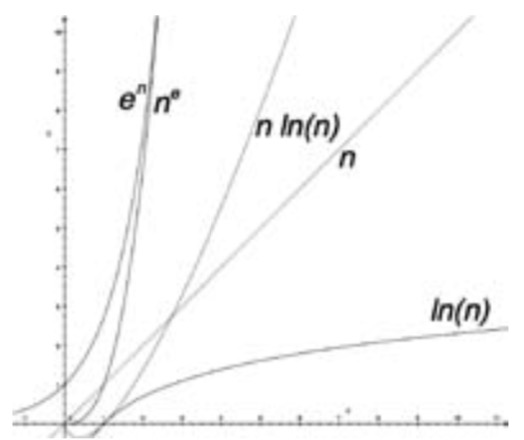
时间和空间复杂度函数给出的O(f(n)),这个n等同于输入参数趋近于无穷时,n增长的时间和空间的情况。主要的f(n)复杂度类别包括:ln(n)、n、n*ln(n)、n^e、e^n等。如下图所示,这些函数表明,档n越大,O(ln(n))总是小于O(n)和O(n*ln(n)),也比O(n^e)和O(e^n)要小得多。正如Sean Parent所说,对于可实现的n,所有复杂度类别中,要么接近常数,要么接近于线性增长,要么接近于无穷。
复杂度的分析是根据抽象机器来衡量的,但软件却运行在真实的机器上。现代计算机系统被组织为物理机和虚拟机两种架构,包括运行语言、操作系统、CPU、缓存、RAM、硬盘、网络等。下表展示了一个典型的网络服务的随机访问时间和存储能力的限制。
| 类型 | 访问时间 | 存储容量 |
|---|---|---|
| 寄存器 | < 1ns | 64b |
| 缓存 | 64B | |
| - 1级缓存 | 1ns | 64KB |
| - 2级缓存 | 4ns | 8M |
| RAM | 20ns | 32GB |
| 磁盘 | 10ms | 10TB |
| 局域网 | 20ms | > 1PB |
| 互联网 | 100ms | > 1ZB |
要注意(不同设备)存储能力和访问速度会有几个数量级的差异。但在我们系统的每个级别都采用大量的缓存和预测来隐藏这种差异,可惜它们只有在访问可预测时才能正常工作。当缓存未命中,系统将发生颠簸。例如,随机检查硬盘的每个字节要花费32年。甚至随机检查RAM的每个字节都要花费11分钟。随机访问时不可预测的,那什么可以?这依赖于系统,但重新访问最近使用和顺序访问才是常态。
算法和数据结构所使用的缓存在效率方面各有不同,例如:
- 线性搜索有比较好的预测,但需要O(n)次比较。
- 二分法搜索排序数组需要O(log(n))次比较。
- van Emde Boas树则需要O(log(n))次和cache-oblivious模型。
如何选择呢?通过最后的分析测量。下表显示了在我的电脑上,通过这三种方法搜索64位整数数组所需时间(纳秒):
| 数组长度 | 线性 | 二分法 | vEB |
|---|---|---|---|
| 8 | 50 | 90 | 40 |
| 64 | 180 | 150 | 70 |
| 512 | 1200 | 230 | 100 |
| 4096 | 17000 | 320 | 160 |
- 线性搜索在小数组时很有竞争力,但在大数组情况下就不行了。
- vEB凭借可预测访问模型赢得胜利。

